1. 버블 정렬

버블 정렬은 보시다시피
두 개씩 비교해서 정렬한다는 모양이 마치
거품과도 같다해서 버블 정렬이라고 부릅니다.
맨 왼쪽에서부터 두 가지 수를 비교해서 오른쪽 수가 적으면 서로 자리를 바꾸고
오른쪽 수가 크면 자리를 바꾸지 않는 것입니다.
저 빨간색 네모가 왼쪽에서 맨 오른쪽까지 도착하게 되면
한 번 순회했다고 부르는데
한 번 순회할 때마다 맨 오른쪽에 하나씩 정렬이 됩니다.
왜냐하면 제일 큰 수는 저 빨간색 네모에서 계속 자리를 바꿔
결국에는 맨 뒤로 향하기 때문입니다.
그래서 한 번 순회하면 ~~, 8
두 번 순회하면 ~~7, 8
여섯 번 순회하면 1, 2, 3, 6, 7, 8
이런 식으로 정렬이 됩니다.
이러한 동작을 코드로 구현하면 다음과 같습니다.
input = [3, 6, 2, 7, 1, 8]
def bubble_sort(array):
n = len(array)
for i in range(n): # N의 크기만큼 반복
for j in range(n - i - 1): # (N - 1) + (N - 2) + ... + 1 반복
if array[j] > array[j + 1]:
array[j], array[j + 1] = array[j + 1], array[j]
return array
input = bubble_sort(input)
print(input)
그러면 버블 정렬의 시간 복잡도를 계산해보자
반복문이 2개 있으므로 O(N²)이 걸린다
다른 대입 연산, 비교 연산은 상수로 빠지니까 생각하지 않는다.
버블 정렬은 다음과 같이 동작한다
옆과 비교하면서 최댓값을 찾아가면서 쌓아지고 연결된다 라고 생각하면 된다.

2. 선택 정렬

선택 정렬은 배열 안에서 가장 최솟값을 찾은 다음
처음으로 배치하는 작업이다.
최솟값을 찾기 위해 배열의 모든 요소를 검사하는 그 작업 한 번을 순회했다 라고 하는데
한 번 순회할 때마다 왼쪽부터 데이터가 하나씩 정렬이 된다.
input = [5, 1, 8, 4, 9, 6, 7, 2, 3]
def selection_sort(array):
n = len(array)
for i in range(n - 1): // N의 크기만큼 반복
min_index = i
for j in range(n - i): // N의 크기만큼 반복
if array[i + j] < array[min_index]:
min_index = i + j
array[i], array[min_index] = array[min_index], array[i]
return array
input = selection_sort(input)
print(input)
이 선택 정렬도 버블 정렬처럼 두 개의 반복문이 있고 각각 N의 크기만큼 반복된다.
위의 gif 파일을 봐도 알 수 있다.
하나의 최솟값 데이터를 찾는데 배열 크기만큼 순회하며
그 순회를 배열 크기만큼 반복해야 한다
각 순회(N) 당 배열 크기(N)만큼 반복 = N * N = O(N²)이 된다.

선택 정렬은 최솟값을 찾아내면서 쌓아지는 형태이다.
3. 삽입 정렬
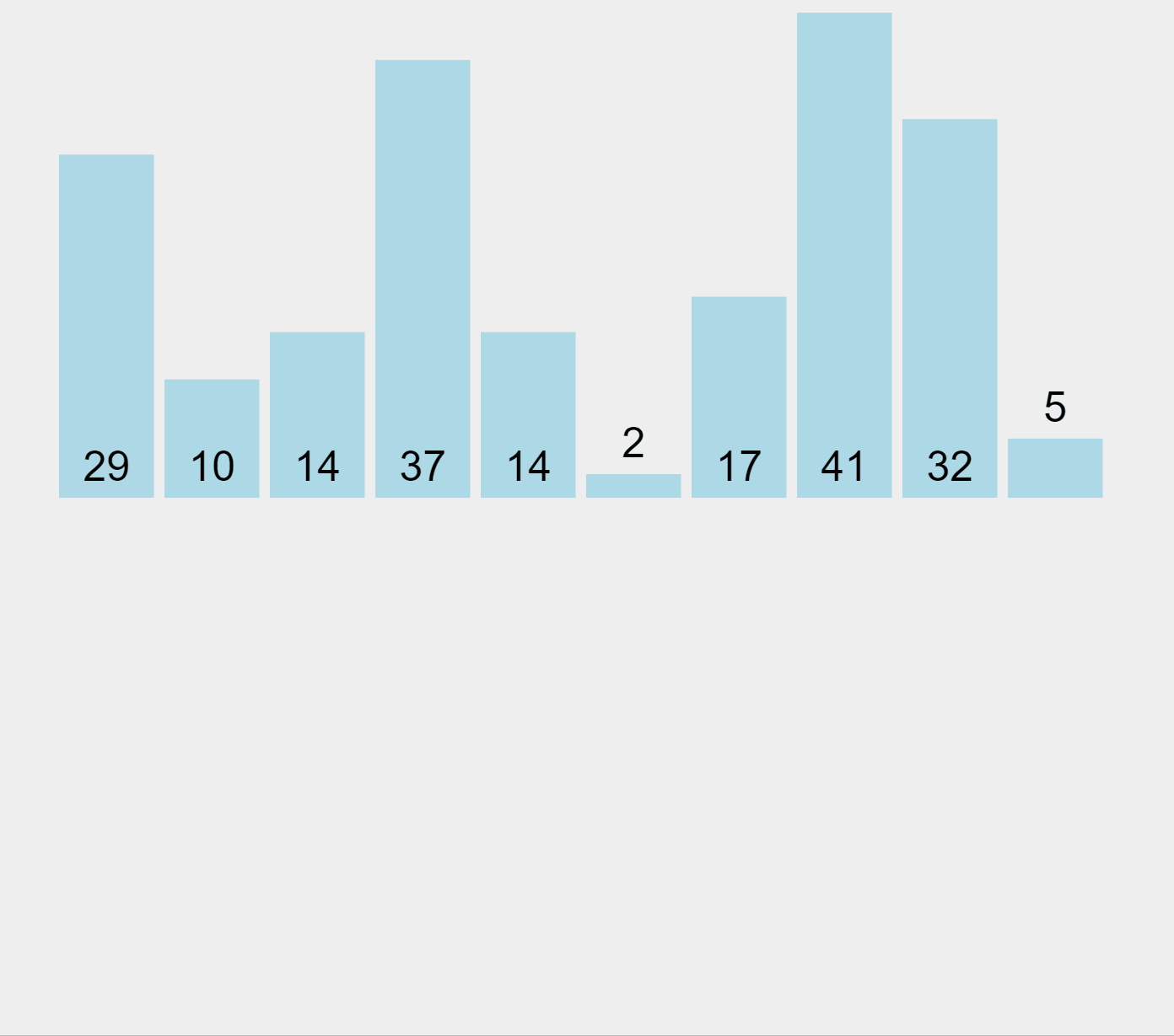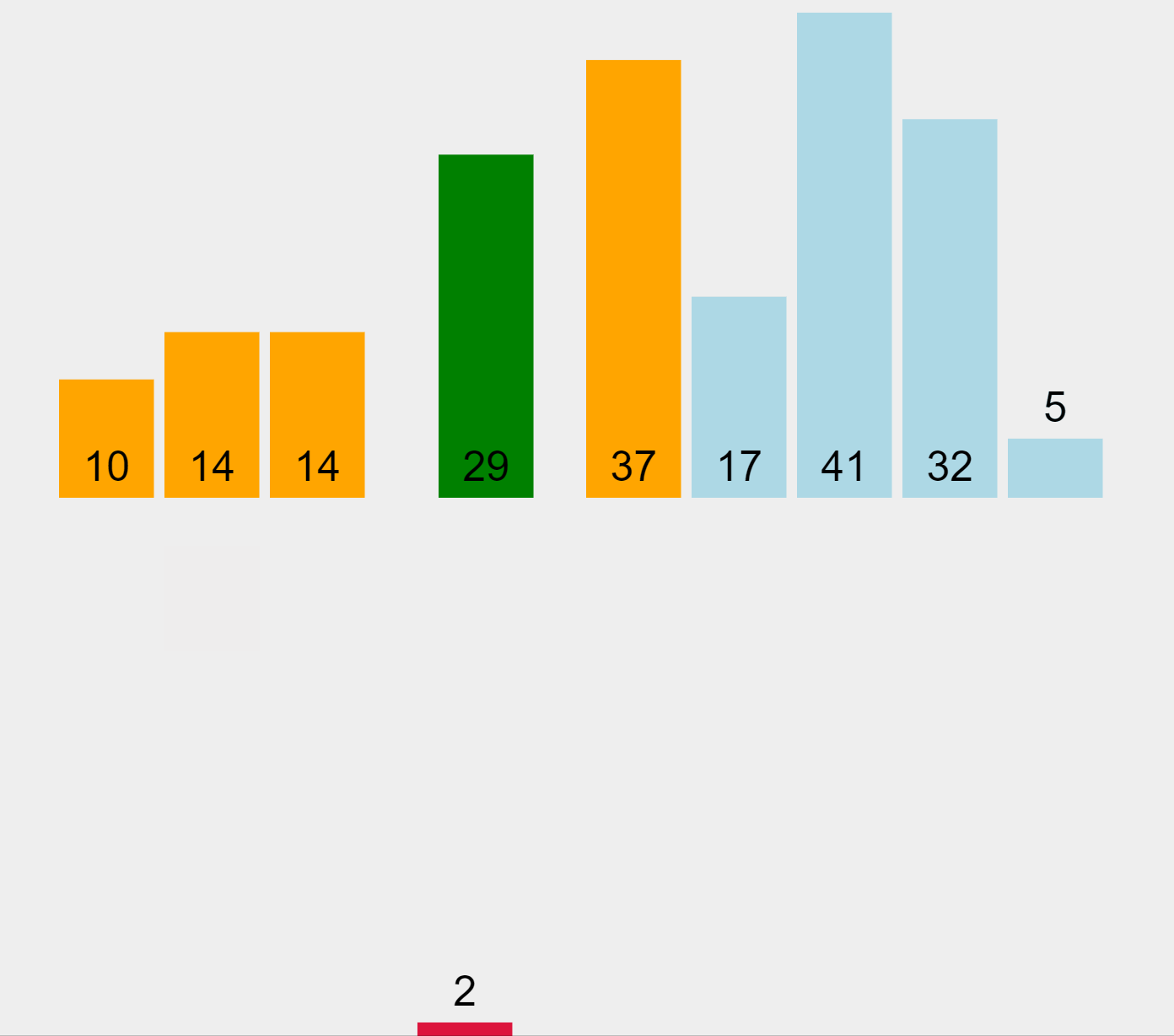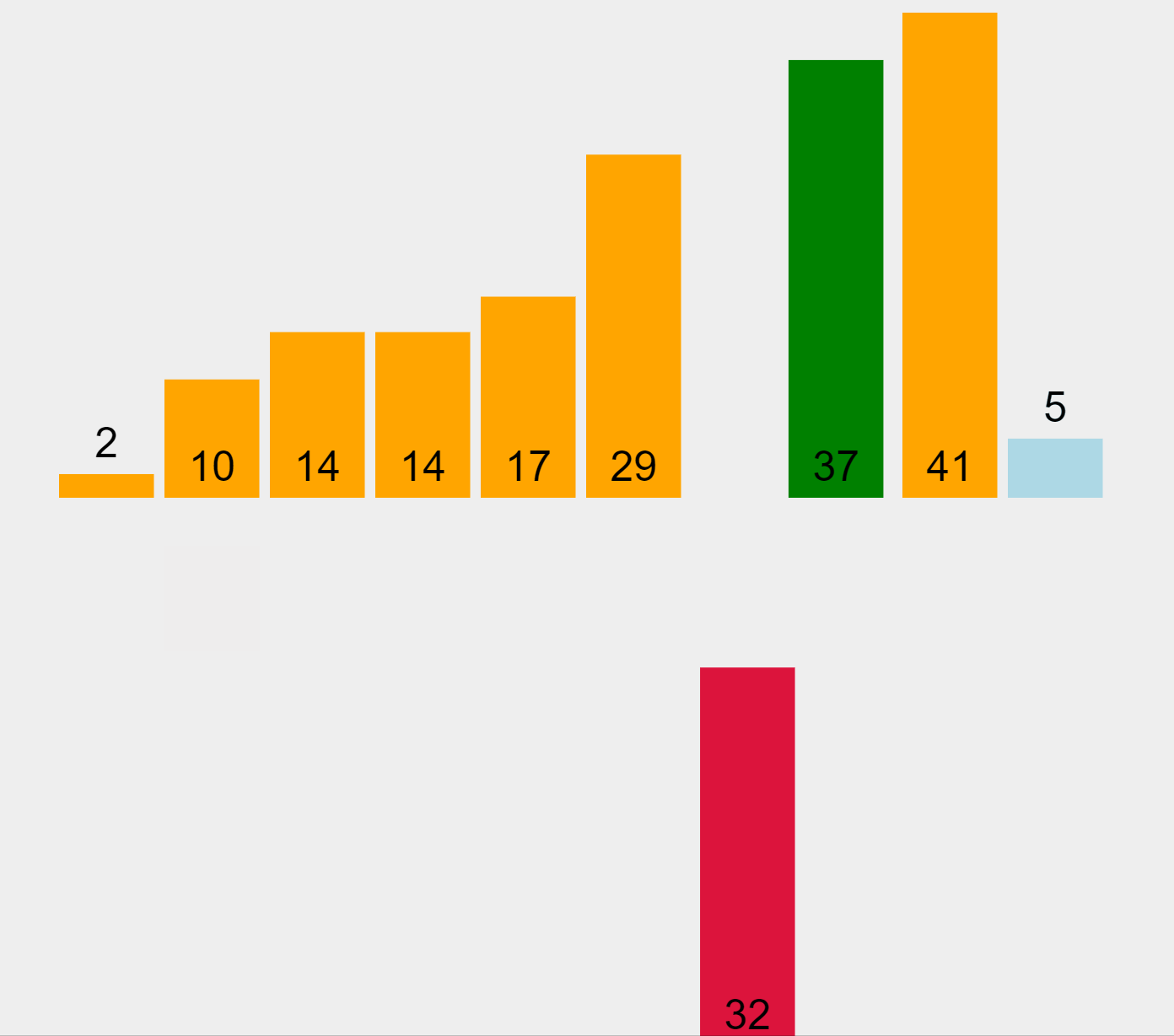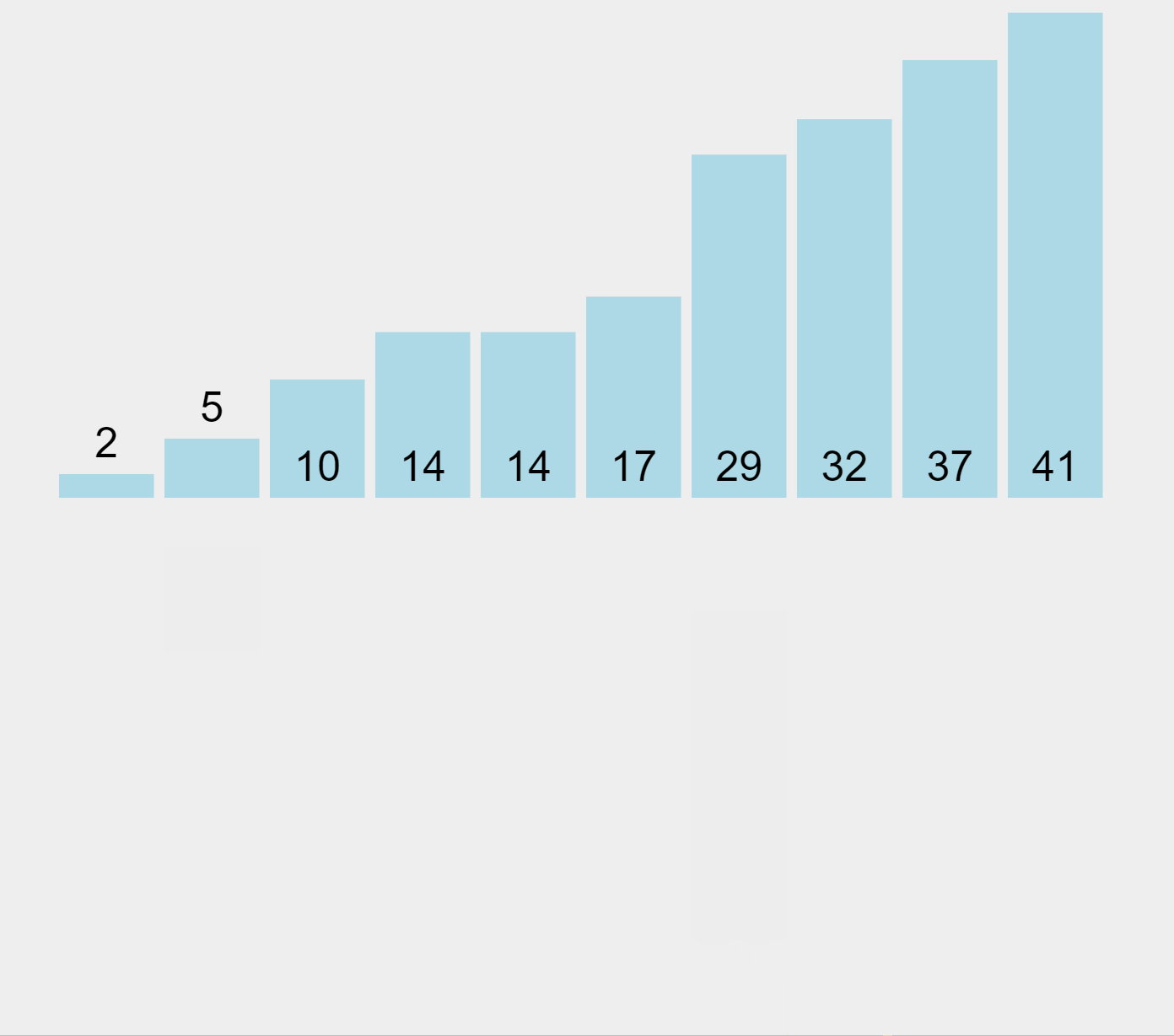
선택 정렬이 전체에서 최솟값을 하나씩 '선택' 하는 거였다면
삽입 정렬은 전체에서 하나씩 올바른 위치에 '삽입'하는 방식이다.
선택 정렬은 현재 데이터의 상태와 상관없이 항상 비교하고 위치를 바꾸지만
삽입 정렬은 필요할 때만 위치를 변경하므로 더 효율적인 방식이다.
input = [29, 10, 14, 37, 14, 2, 17, 41, 32, 5]
def insertion_sort(array):
n = len(array)
for i in range(1, n):
for j in range(i):
if array[i - j - 1] > array[i - j]:
array[i - j - 1], array[i - j] = array[i - j], array[i - j - 1]
else:
break
return array
input = insertion_sort(input)
print(input)
삽입 정렬은 버블 정렬과 선택 정렬과는 다른 점이 있습니다
최악의 경우에선 O(N²)이 걸리지만
최선의 경우에는 Ω(N)이 걸립니다.
왜냐하면 모든 데이터가 이미 정렬된 상태라면 위치를 옮기는 과정이 없고
바로 왼쪽에 데이터 하고만 비교하는 과정인 (N)만 있기 때문입니다.

데이터들이 제자리를 찾아가면서 쌓아지는 형태이다.
'이론 > 알고리즘' 카테고리의 다른 글
| [알고리즘] DFS (Depth First Search) (0) | 2021.09.17 |
|---|---|
| [알고리즘] 병합정렬을 그림으로 알아보자 (0) | 2021.09.16 |
| [알고리즘] 재귀함수 (0) | 2021.08.21 |
| [알고리즘] 이진탐색 시간복잡도 (0) | 2021.08.21 |
| [알고리즘] 시간복잡도, 공간복잡도, 점근표기식 (0) | 2021.08.15 |