책 읽다가 코딩하다 죽을래
알고보면 알기쉬운 알고리즘 - 4주차 개발일지(트리, 힙, 그래프, DFS&BFS, DP) 본문
GD프로젝트 알고리즘 수업 4주 차가 시작되었다.
그럼 4주 차에 배운 내용과 풀었던 알고리즘 문제에 대해 설명하겠다.
목차
1. 새롭게 배운 내용(트리, 힙, 그래프, DFS, BFS, Dynamic Programming)
2. CGV 극장 좌석 자리 구하기 문제
1. 새롭게 배운 내용
1 - 0 선형, 비선형
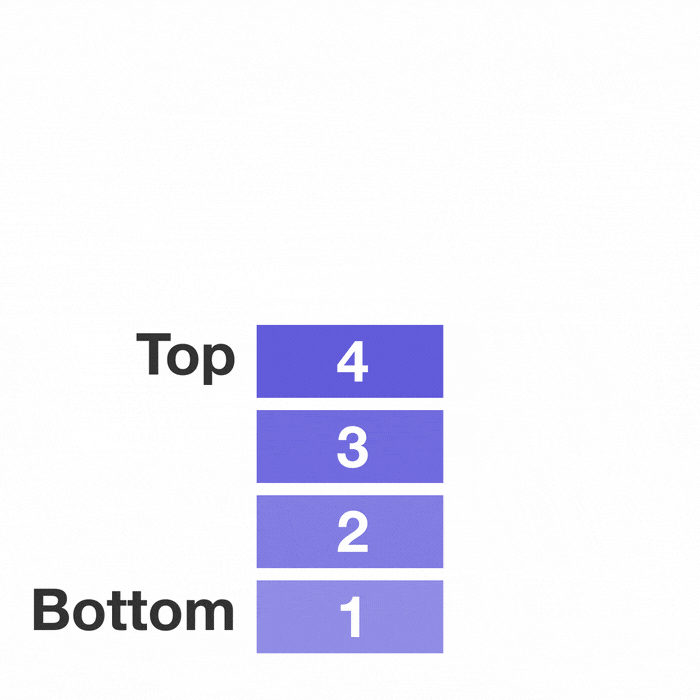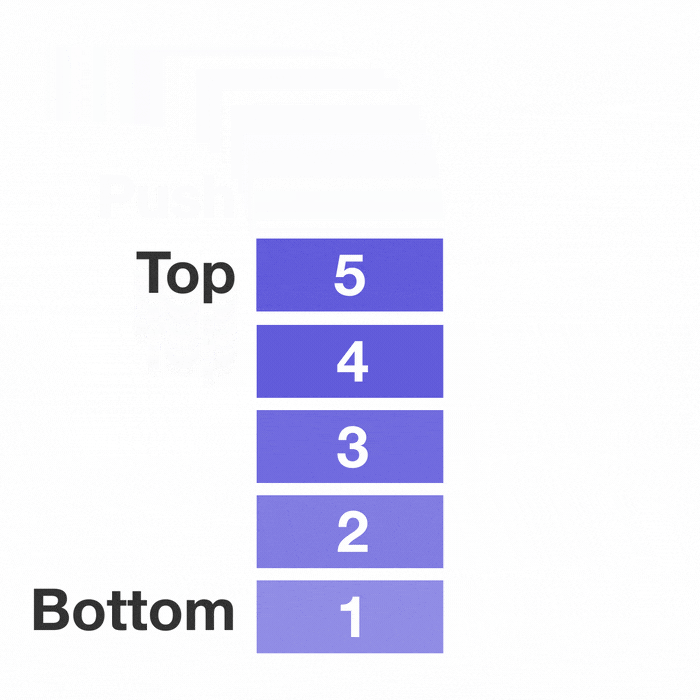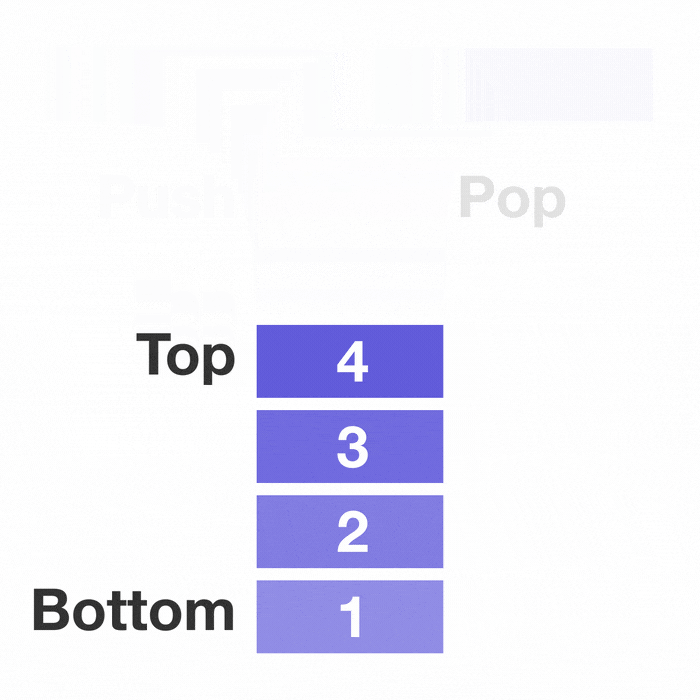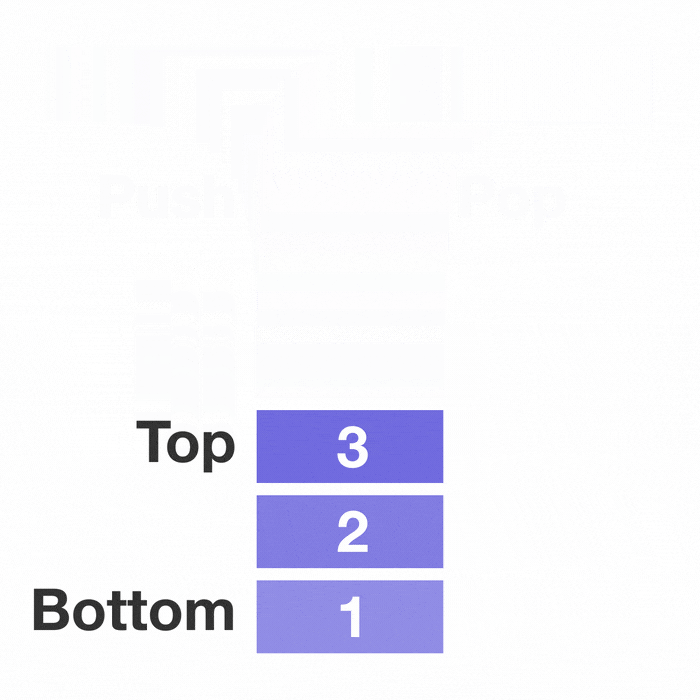
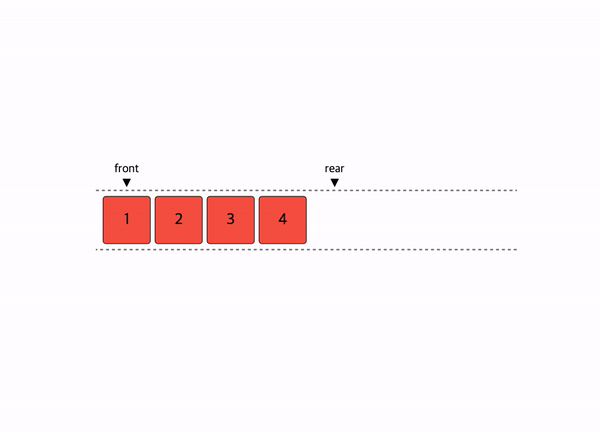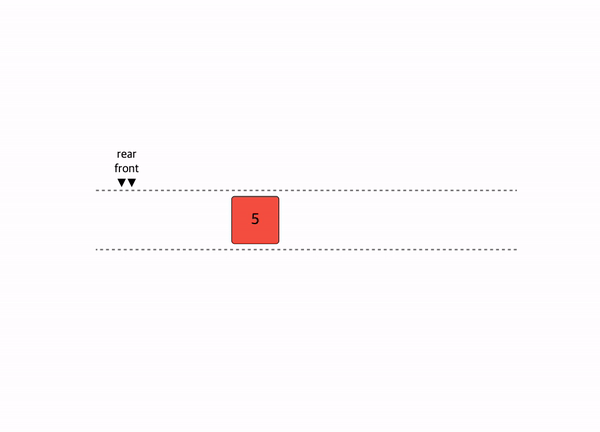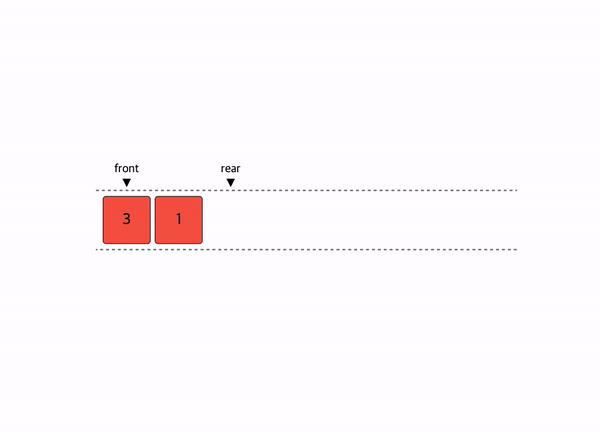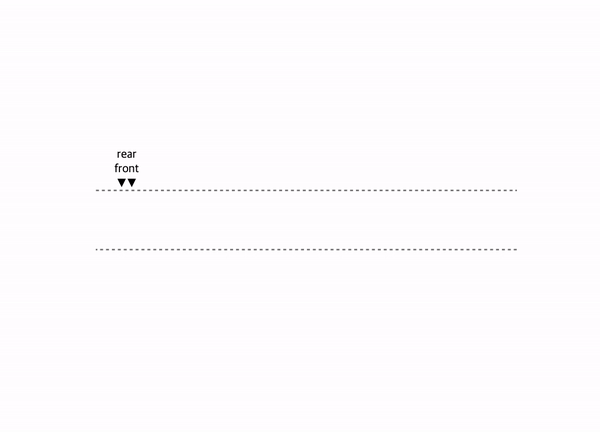
선형 자료구조의 대표적인 예시인 스택과 큐이다.
선형구조는 처음과 끝이 확연히 정해져 있다.
그래서 자료를 저장하고 꺼내고 탐색하는 것에 초점이 맞추어져 있다.
즉 내가 사용해야할 자료구조가 조회, 삽입, 삭제가 얼마나 빈번하냐에 따라
선택해야 한다.
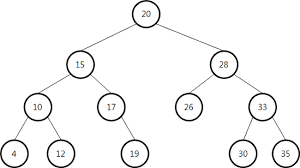
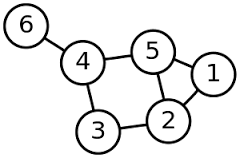
비선형 자료구조의 대표적인 예시인 트리와 그래프이다.
비선형 구조는 처음과 끝이 정해져 있지 않으며
때로는 순환적이기도 하다.
비선형 자료구조는 표현에 초점이 맞춰져 있다.
즉 내가 사용해야 할 자료구조를 어떤 식으로 표현할 거냐에 따라
선택해야 한다.
1 - 1 트리
트리는 뿌리와 가지로 구성되어 거꾸로 세워놓은 나무처럼 보이는 계층형 비선형 자료 구조이다.
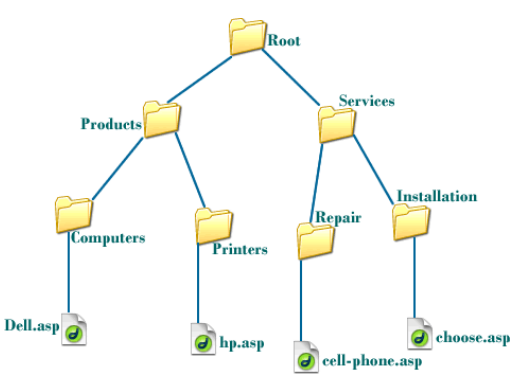
트리는 대표적인 사용 예시는 컴퓨터의 폴더 구조이다.
파일이 어느 경로에 있는지 그 경로에는 어떤 폴더들이 포함되는지 나타내야 하기 때문이다.
트리의 구조는 다음과 같다
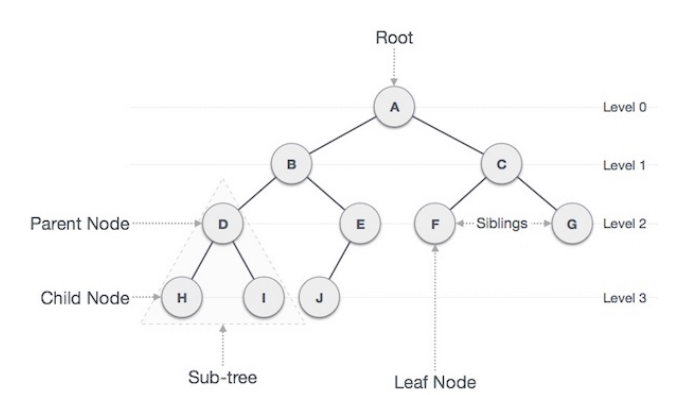
Node : 트리에서 데이터를 저장하는 기본 요소
Root Node : 트리 맨 위에 있는 노드
Level : 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
Parent Node : 어떤 노드의 상위 레벨에 연결된 노드
Child Node : 어떤 노드의 하위 레벨에 연결된 노드
Leaf Node(Terminal Node) : Child Node가 하나도 없는 노드
Sibling : 동일한 Parent Node를 가진 노드
Depth : 트리에서 Node가 가질 수 있는 최대 Level
이진 트리(Binary Tree)
트리의 대표적인 종류 중 하나인 이진트리의 특징은
각 노드가 최대 두 개의 자식을 가진다.
Child Node가 3개 이상 가질 수 없으며
무조건 0,1,2 개로만 있어야 한다.
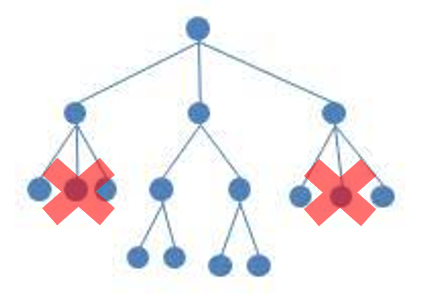
완전 이진 트리(Complete Binary Tree)
완전 이진트리의 특징은 노드를 삽입할 때 최하단 왼쪽 노드부터 차례대로 삽입해야 하는 것이다.
완전 이진 트리의 표현법은 대체로 배열로 표현한다
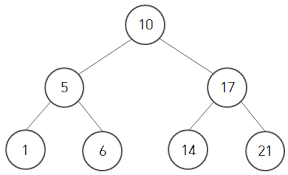
# 10
# 5 17
# 1 6 14 21
tree = [None, 10, 5, 17, 1, 6, 14, 21]
# 첫 인덱스는 None으로 비워준다. 계산하기 편하기 위해 일부터 비워두는 것이다.완전 이진트리라는 전제 하에
왼쪽에서부터 오른쪽으로
위에서 아래로 하나씩 차례대로 넣는 것이다.
이런 식으로 배열에 넣게 되면 부모와 자식 사이의 인덱스 관계가 공식에 따라 성립한다.
1. 현재 인덱스 * 2 -> 왼쪽 자식의 인덱스
2. 현재 인덱스 * 2 + 1 -> 오른쪽 자식의 인덱스
3. 현재 인덱스 // 2 -> 부모의 인덱스
즉 현재 인덱스가 3인 17은
3 // 2 = 1
인덱스가 1인 10의 자식 노드이다
현재 인덱스가 2인 5는
2 * 2 = 4
인덱스가 4인 1의 부모 노드(왼쪽 자식)이다.
현재 인덱스가 2인 5는
2 * 2 + 1= 5
인덱스가 5인 6의 부모 노드(오른쪽 자식)이다.
완전 이진트리의 높이
각 level을 k라고 한다면 각 level에 최대로 들어갈 수 있는 노드의 개수는 2^k 개수 임을 알 수 있다.
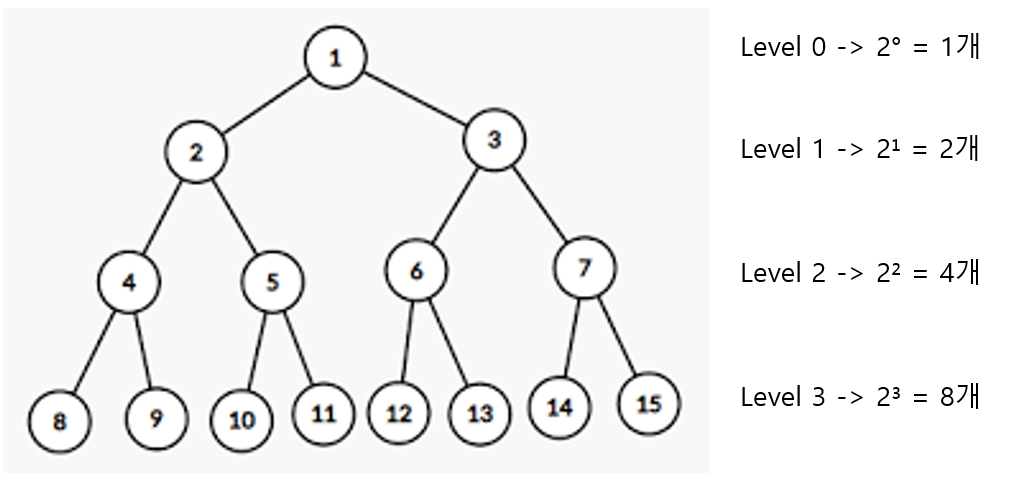
level k 에선 2^k 만큼의 노드가 있는 것이다.
만약 높이가 h라면 모든 노드의 개수는 몇 개 일까?
1 + 2¹ + 2² + 2³ + ... + 2^h 이니
2^(h+1) - 1 이 된다.
높이가 h일 때 최대 노드의 개수는 2(h + 1) - 1 개
최대 노드의 개수가 N이라면
2(h + 1) -1 = N
h = log₂(N+1) - 1
완전 이진트리 노드의 개수가 N일 때 최대 높이가 log₂(N+1) - 1 이므로
어떤 트리의 노드를 모두 탐색해야 되는 경우 O(log(N)) 이 된다
1 - 2 힙
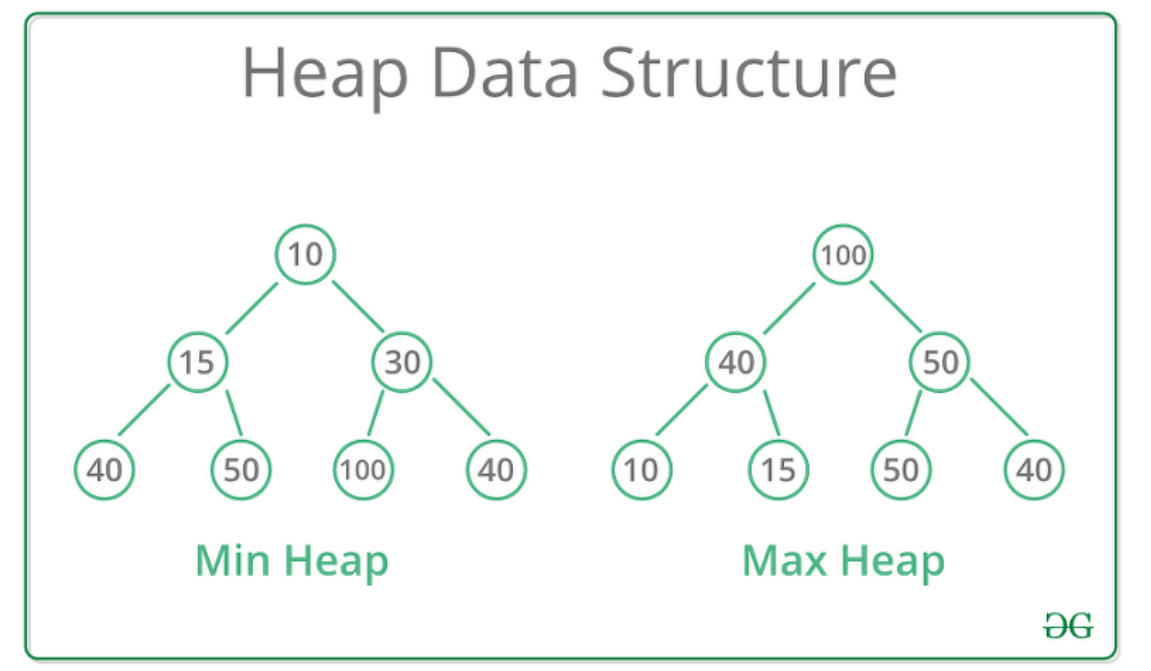
힙은 데이터에서 최댓값과 최솟값을 찾기 위해 고안된 완전 이진 트리이다.
힙은 항상 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있도록 하는 자료구조이다.
즉 부모 노드의 값이 자식 노드의 값보다 항상 커야 한다.
그러면 가장 큰 값이 모든 자식보다 크기 때문에 가장 위로 간다.
바로 루트 노드로 말이다.
이렇게 아래로 갈수록 작고 위로 갈수록 커지는 힙은 Max Heap이라 하고
이와 반대인 경우는 Min Heap이라 한다.
그런데 힙은 항상 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있어야 하는 규칙이 있다.
그러면 힙에 새로운 노드를 삽입하거나 이미 존재하는 노드를 삭제할 때
규칙을 어기지 않게 하려면 어떻게 해야 할까?
노드 삽입
노드 삽입 과정은 이렇다.

MaxHeap의 삽입 과정을 다음과 같다.
1. 원소를 맨 마지막에 넣는다.
2. 부모 노드와 비교한다. 만약 크다면 자리를 바꾼다.
3. 부모 노드보다 작거나 가장 위에 도달하지 않을 때까지 2. 과정을 반복한다.
코드로 구현하면 다음과 같다.
class MaxHeap:
def __init__(self):
self.items = [None]
def insert(self, value):
self.items.append(value)
aryLen = len(self.items)
if aryLen < 3 : return
compareIndex = aryLen - 1
while 1 < compareIndex:
if self.items[compareIndex] < self.items[compareIndex // 2]: break
self.items[compareIndex], self.items[compareIndex // 2] = self.items[compareIndex // 2] , self.items[compareIndex]
compareIndex = compareIndex // 2
max_heap = MaxHeap()
max_heap.insert(3)
max_heap.insert(4)
max_heap.insert(2)
max_heap.insert(9)
print(max_heap.items) # [None, 9, 4, 2, 3] 가 출력되어야 합니다!
여기서 우리는 노드 삽입에 담당하는 insert함수의 시간 복잡도를 알아봐야 한다.
이진트리의 최대 높이는 O(log(N))이다
insert 함수 안에 while 반복문은 최대 트리의 높이만큼 반복된다.
그러므로 insert함수의 시간복잡도는 O(log(N)) 이다.
노드 삭제
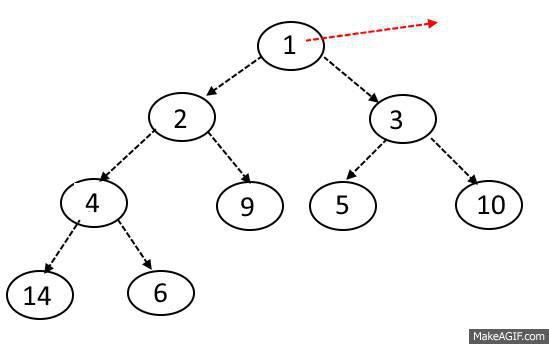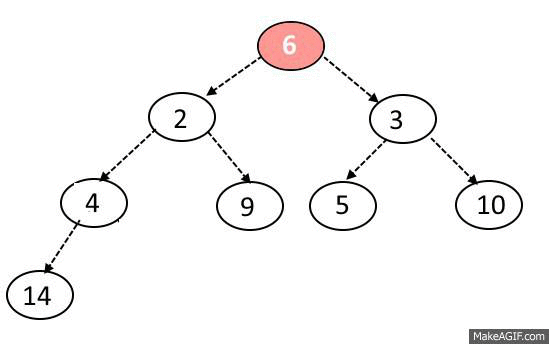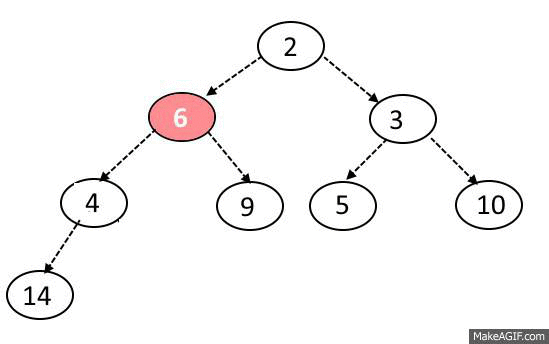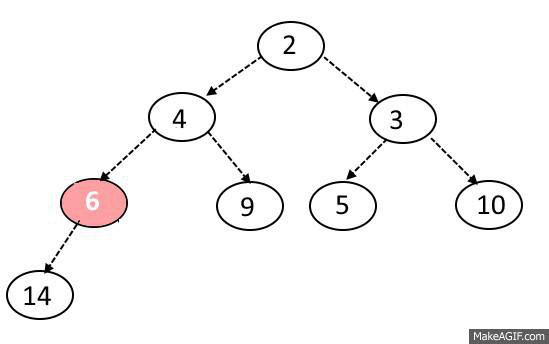
MaxHeap의 삭제 과정을 다음과 같다.
노드 삭제는 오로지 루트 노드만 제거할 수 있다.
또한 원소를 삭제할 때도 힙의 규칙이 지켜져야 한다.
노드 삭제 방법은 다음과 같다.
1. 루트 노드와 맨 끝에 있는 원소를 교체한다.
2. 맨 뒤에 있는 원소를 (원래 루트 노드)를 삭제한다.
3. 변경된 노드와 자식 노드들을 비교한다.
두 자식 중 더 큰 자식과 비교해서 더 크다면 자리를 바꾼다.
4. 자식 노드 둘 보다 부모 노드가 크거나 가장 바닥에 도달하지 않을 때까지 3. 과정을 반복한다.
5. 2에서 제거한 원래 루트 노드를 반환한다.
코드로 구현하면 다음과 같다.
class MaxHeap:
def __init__(self):
self.items = [None]
def insert(self, value):
self.items.append(value)
cur_index = len(self.items) - 1
while cur_index > 1: # cur_index 가 1이 되면 정상을 찍은거라 다른 것과 비교 안하셔도 됩니다!
parent_index = cur_index // 2
if self.items[parent_index] < self.items[cur_index]:
self.items[parent_index], self.items[cur_index] = self.items[cur_index], self.items[parent_index]
cur_index = parent_index
else:
break
# 1. 루트 노드와 맨 끝에 있는 원소를 교체한다.
# 2. 맨 뒤에 있는 원소를 (원래 루트 노드)를 삭제한다. 이 때, 끝에 반환해줘야 하니까 저장한다.
# 3. 변경된 노드와 지식 노드들을 비교합니다. 두 자식 중 더 큰 자식과 비교해서 자신보다 자식이 더 크다면 자리를 바꾼다.
# 4. 자식 노드들 보다 부모 노드가 더 크거나 가장 바닥에 도달하지 않을때까지 3. 을 반복한다.
# 5. 2에서 제거한 원래 루트 노드를 반환한다.
def delete(self):
aryLen = len(self.items)
# 2.
delete_node = self.items[1]
# 1.
self.items[1] = self.items[aryLen - 1]
del self.items[aryLen - 1]
compareIndex = 1
# 3. 4.
while compareIndex < aryLen:
if self.items[compareIndex * 2] < self.items[compareIndex * 2 + 1] and self.items[compareIndex] < self.items[compareIndex * 2 + 1]:
self.items[compareIndex] , self.items[compareIndex * 2 + 1] = self.items[compareIndex * 2 + 1] , self.items[compareIndex]
elif self.items[compareIndex * 2 + 1] < self.items[compareIndex * 2] and self.items[compareIndex] < self.items[compareIndex * 2]:
self.items[compareIndex], self.items[compareIndex * 2] = self.items[compareIndex * 2], self.items[compareIndex]
else : break
# 5.
return delete_node # 8 을 반환해야 합니다.
max_heap = MaxHeap()
max_heap.insert(8)
max_heap.insert(6)
max_heap.insert(7)
max_heap.insert(2)
max_heap.insert(5)
max_heap.insert(4)
print(max_heap.items) # [None, 8, 6, 7, 2, 5, 4]
print(max_heap.delete()) # 8 을 반환해야 합니다!
print(max_heap.items) # [None, 7, 6, 4, 2, 5]
삭제 과정의 시간복잡도 또한 O(log(N))이다.
반복문이 최대 완전 이진트리의 최대 높이만큼 반복되기 때문이다.
1 - 3 그래프
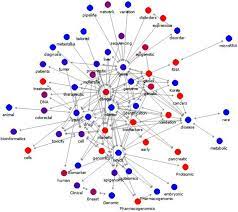

그래프는 연결되어 있는 정점과 정점 간의 관계를 표현할 수 있는 비선형 자료구조이다.
그래프는 TCP 라우팅 알고리즘과 페이스북 관계망 등에서 자주 쓰이는 자료구조이다.
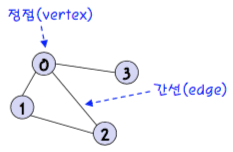
그래프는 다음의 요소들을 갖고 있다.
노드(Node) : 연결 관계를 가진 각 데이터를 의미한다. 정점(Vertex)라고도 한다.
간선(Edge) : 노드 간의 관계를 표시한 선
인접 노드(Adjacent Node) : 간선으로 직접 연결된 노드(또는 정점)
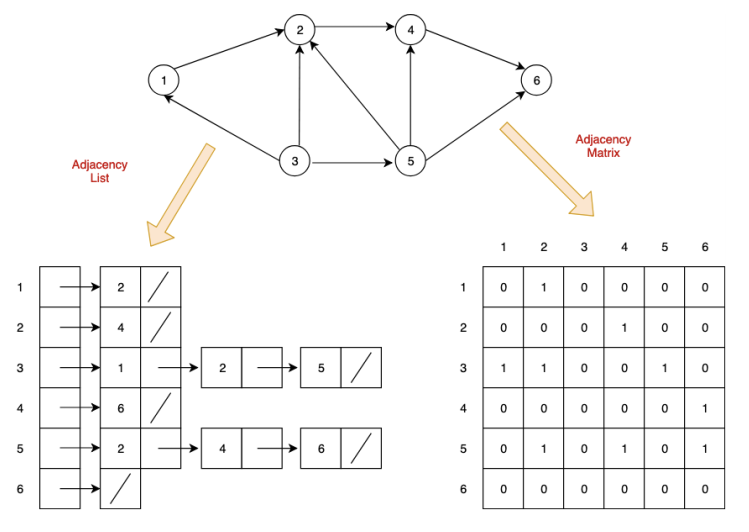
그래프를 코드로 표현하는 방법은 LinkedList와 Array가 있는데
LinkedList는 각 정점간의 관계를 노드로 연결하여 표현한다.
서로 연결된 정점끼리 노드로 연결되어 있는 것이다.
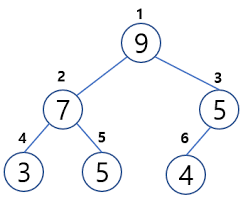
위에 사진을 예로 들면 3번과 연결되어 있는 정점들을 보려면
head를 3으로 가리킨 후 계속 다음 데이터를 가리키는 쪽으로 따라가면
1, 2, 5 번이 있다는 것을 알 수 있다.
Array는 각 정점 간의 관계를 이차원 배열로 나타내
서로 연결되어 있으면 1(True)을
서로 연결되어 있지 않으면 0(False)으로 나타낸다
위에 사진을 예로 들면 정점 1번에서 정점 2번간의 관계를 보려면
인덱스 [0][1] = 1 (1번에서 2번으로 연결되어 있음)
인덱스 [1][0] = 0 (2번에서 1번으로 연결되어 있지 않음)
를 보면 된다.
LinkedList는 Array보다는 공간복잡도가 적은 대신 데이터 탐색 시간복잡도는 크지만
Array는 LinkedList보다는 데이터 탐색 시간복잡도는 작지만 공간복잡도가 크다
1 - 4 DFS (Depth First Search)
DFS는 자료의 검색 트리나 그래프를 탐색하는 방법 중 하나이다. 한 노드를 시작으로 인접한 다른 노드를 재귀적으로 탐색해가고 끝까지 탐색하면 다시 위로 와서 다음을 탐색하여 검색한다.
DFS는 이름에 나와있는 그대로 끝까지 탐색하는 거에 초점을 맞춘다.
그래서 그래프의 최대 깊이만큼의 공간을 요구하며, 이는 공간을 적게 쓰는 것이다.
그러나 최단 경로를 탐색하기는 쉽지 않다. 모든 경로를 탐색하는 것이 아니기 때문이다.
DFS의 알고리즘 방식을 설명하면 다음과 같다.
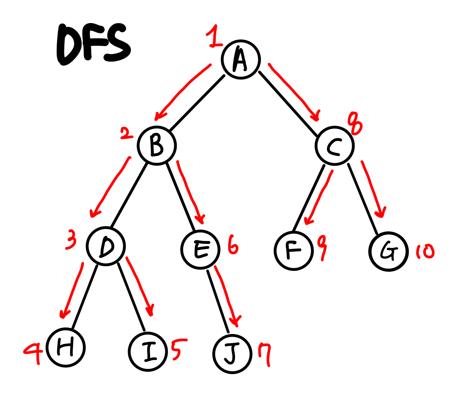
1. 노드를 방문하고 깊이 우선으로 인접한 노드를 방문한다.
2. 또 그 노드를 방문해서 깊이 우선으로 인접한 노드를 방문한다.
3. 만약 끝에 도달했다면 리턴한다.
이를 코드로 구현하려면 자료구조 스택을 사용하시는 것이 편리합니다
스택을 사용하면 방법은 다음과 같습니다.
1. 루트 노드를 스택에 넣는다.
2. 현재 스택의 노드를 빼서 visited(또 다른 배열)에 추가한다.
3. 현재 방문한 노드와 인접한 노드 중 방문하지 않은 노드를 스택에 추가한다.
4. 2부터 반복한다.
5. 스택에 아무것도 없으면 탐색을 종료한다.
# 위의 그래프를 예시로 삼아서 인접 리스트 방식으로 표현했습니다!
graph = {
'A' : ['B', 'C'],
'B' : ['A', 'D', 'E'],
'C' : ['A', 'F', 'G'],
'D' : ['B', 'H', 'I'],
'E' : ['B', 'J'],
'F' : ['C'],
'G' : ['C'],
'H' : ['D'],
'I' : ['D'],
'J' : ['E'],
}
visited = []
# 1. 시작 노드를 스택에 넣습니다
# 2. 현재 스택의 노드를 빼서 visited 에 추가한다.
# 3. 현재 방문한 노드와 인접한 노드 중에서 방문하지 않은 노드를 스택에 추가한다.
def dfs_stack(adjacent_graph, start_node):
stack = [start_node]
while stack:
current_node = stack.pop()
visited.append(current_node)
for value in adjacent_graph[current_node]:
if value not in visited:
stack.append(value)
return visited
print(dfs_stack(graph, 'A')) # 'A' 이 시작노드입니다!
# ['A', 'C', 'G', 'F', 'B', 'E', 'J', 'D', 'I', 'H'] 이 출력되어야 한다!
스택으로 구현하게 되므로 맨 뒤에서부터 탐색하게 된다.
위에 그림상에선 A 다음 B를 탐색하지만
이 코드는 A 다음 B, C 중에 뒤에 있는 C부터 탐색한다는 것이다.
C를 탐색하면 스택에는 B, A, F, G가 있으니 G를 탐색하면
B, A, F, C 가 돼야 하는데 C는 이미 탐색을 해서
B, A, F 만 된다.
이렇게 반복되면 DFS 절차에 맞게 탐색되는 것이다.
1 - 5 BFS
한 노드를 시작으로 인접한 모든 정점들을 우선 방문하는 방법이다. 더 이상 방문하지 않은 정점이 없을 때까지 방문하지 않은 모든 정점들에 대해서 넓이 우선 검색을 적용한다.
DFS는 인접한 한 노드를 끝까지 탐색했다면 BFS는 인접한 모든 정점을 방문한다.
이걸 다시 말하면 인접한 노드 중 방문하지 않은 모드 노드들을 저장하고,
가장 처음에 넣은 노드를 꺼내서 탐색하면 된다.
처음에 넣은 노드이므로 큐를 이용해서 BFS를 구현할 수 있다.
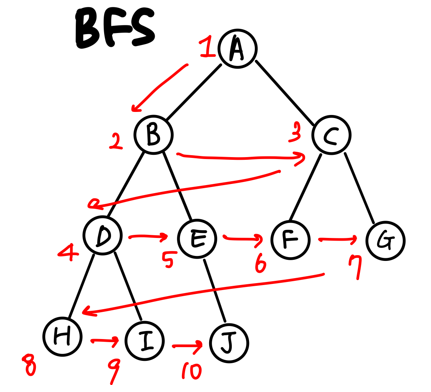
1. 루트 노드를 큐에 넣는다
2. 현재 큐의 노드를 빼서 visited에 추가한다.
3. 현재 방문한 노드와 인접한 노드 중 방문하지 않은 노드를 큐에 추가한다.
4. 2부터 반복한다.
5. 큐가 비면 탐색을 종료한다.
# 위의 그래프를 예시로 삼아서 인접 리스트 방식으로 표현했습니다!
graph = {
'A' : ['B', 'C'],
'B' : ['A', 'D', 'E'],
'C' : ['A', 'F', 'G'],
'D' : ['B', 'H', 'I'],
'E' : ['B', 'J'],
'F' : ['C'],
'G' : ['C'],
'H' : ['D'],
'I' : ['D'],
'J' : ['E'],
}
# DFS와 비슷하다 그냥 스택을 쓰냐 큐를 쓰냐의 차이다.
# 1. 시작 노드를 큐에 넣습니다
# 2. 현재 큐의 노드를 빼서 visited 에 추가합니다
# 3. 현재 방문한 노드와 인접한 노드 중에서 방문하지 않은 노드를 스택에 추가한다.
def bfs_queue(adj_graph, start_node):
queue = [start_node]
visited = []
while queue:
current_node = queue[0]
# current_node = queue.pop(0) 이렇게 뽑아와도 된다.
del queue[0:1]
visited.append(current_node)
for value in adj_graph[current_node]:
if value not in visited:
queue.append(value)
return visited
print(bfs_queue(graph, 'A')) # 1 이 시작노드입니다!
# ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J'] 이 출력되어야 합니다.
기억하자 DFS는 스택 BFS는 큐
1 - 6 Dynamic Programming
동적 계획법이라고 한다.
이것을 설명하기 전에 피보나치수열에 대해 설명하고자 한다.
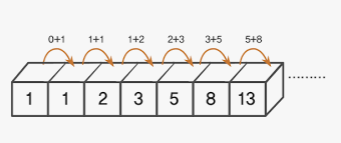
수학에서, 피보나치 수(영어: Fibonacci numbers)는 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다. 처음 여섯 항은 각각 1, 1, 2, 3, 5, 8이다.
그러면 피보나치수열의 몇 번째 항을 바로 알 수 있는 코드를 짜려면 어떻게 해야 할까
첫 번째와 두 번째는 무조건 1이고
다음 항부터는
Fibo(n) = Fibo(n - 1) + Fibo(n - 2)
이 반복된다.
우리는 이것을 재귀 함수로 쉽게 풀 수 있다.
input = 20
# Fibo(N) = Fibo(N - 1) + Fibo(N - 2)
# Fibo(1) = Fibo(2) = 1
def fibo_recursion(n):
if n == 1 or n == 2: return 1
return fibo_recursion(n - 1) + fibo_recursion(n - 2)
print(fibo_recursion(input)) # 6765
그런데 문제가 하나 있다.
입력값을 20이 아닌 100을 한 번 주어 보면 콘솔 창에 아무것도 안 뜨는 것을 볼 수 있다.
이는 동작을 안 하는 것이 아니고 무한 루프를 도는 것도 아니다.
연산량이 엄청 많아 아무리 빠른 컴퓨터라도 시간이 오래 걸려 아직 결과가 안 나온 것이다.
겨우 100을 넣었는데도 왜 이렇게 오래 걸리나 생각해보자
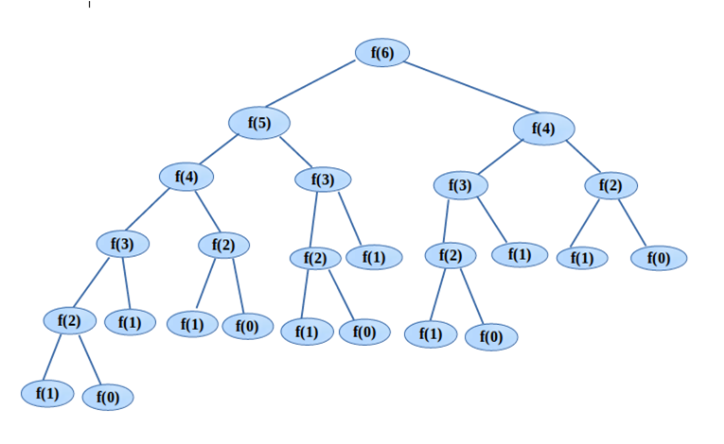
그것은 피보나치수열을 구하는 과정에 있다.
다음 사진은 피보나치의 7번째 인덱스를 구하기 위해 함수 스택을 정리한 것이다.
F(6)을 하면 재귀 함수에 의해 F(5)와 F(4)가 호출된다.
또 F(5)는 F(4)를 호출시킨다.
근데 이 사진을 보면 똑같은 연산이 많다는 것을 느껴진다.
F(1)을 한 번 연산하면 그 결과를 어디엔가 저장하고
그 후에는 F(1)이 호출될 때마다 연산하지 않고 그 결과를 불러와서 바로 반환할 수 없는가?
이럴 때 사용되는 것이 DP 동적 계획법이다.
똑같은 연산이 많으면 그것의 결과를 어디엔가 저장해서 다음 연산 때 연산을 스킵하고
그 결과를 바로 주는 것
이러한 방법은 메모이제이션(Memoiztion)이라 하고 많은 응용 프로그램 또는 시스템, 애플리케이션에 속도를 빠르게 하기 위해 쓰인다.
그럼 아까 피보나치수열을 DP로 풀어보는 과정을 알아보자
1. 메모용 데이터를 만든다. 처음 값인 Fibo(1), Fibo(2)는 각각 1씩 넣어서 저장한다.
2. Fibo(n) 을 구할 때 만약 메모에 그 값이 있다면 바로 반환한다.
3. Fibo(n) 을 처음 구했다면 메모에 그 값을 기록한다.
input = 100
# memo 라는 변수에 Fibo(1)과 Fibo(2) 값을 저장해놨습니다!
memo = {
1: 1,
2: 1
}
# 1. 만약 메모에 있으면 그 값을 바로 반환하고
# 2. 없으면 아까 수식대로 구한다.
# 3. 그리고 그 값을 다시 메모에 기록한다.
def fibo_dynamic_programming(n, fibo_memo):
if n in fibo_memo : return fibo_memo[n]
elif n - 1 in fibo_memo and n - 2 in fibo_memo : fibo_memo[n] = fibo_memo[n - 1] + fibo_memo[n - 2]
return fibo_dynamic_programming(n - 1, fibo_memo) + fibo_dynamic_programming(n - 2, fibo_memo)
print(fibo_dynamic_programming(input, memo))
# 354224848179261915075 가 나와야 한다!
아까 한참 오래 걸렸던 100을 다시 입력하면 바로 값이 나오는 것을 알 수 있다.
2. CGV 극장 좌석 자리 구하기 문제

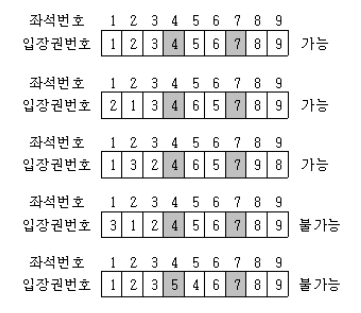
일단 규칙을 찾아보자
좌석 [1] 을 옮기는 경우의 수 [1] -> 1가지
좌석 [1,2] 을 옮기는 경우의 수 [1,2], [2,1] -> 2가지
좌석 [1,2,3] 을 옮기는 경우의 수 [1,2,3], [1,3,2], [2,1,3] -> 3가지
좌석 [1,2,3,4] 을 옮기는 경우의 수 [1,2,3,4], [1,2,4,3], [2,1,3,4], [2,1,4,3], [1,3,2,4] -> 5가지
좌석 [1,2,3,4,5] 을 옮기는 경우의 수 [1,2,3,4,5], [1,2,3,5,4], [2,1,3,4,5], [2,1,3,5,4], [1,2,4,3,5], [2,1,4,3,5], [2,1,3,4,5], [1,3,2,4,5] -> 8가지
1 -> 2 -> (1 + 2) -> (2 + 3) -> (3 + 5) -> ... 약간 증감하는 수가 피보나치와 닮았다고 생각이 든다.
첫 번째 두 번째 항은 1,2 로 고정하고 그때부터 n항은 (n-1) + (n - 2)의 결과를 불러오면 된다
당연히 동적 계획법 방법을 써서 계산한 결과들을 저장하고 나중에 반영해야 한다.
근데 이 문제에선 변수가 하나 있다.
바로 VIP 좌석이다.
VIP는 고정석이라 생각하고 나머지 일반석을 생각해서 구하면 된다.
예로 들면
VIP 가 4,7 이고 좌석은 총 9개 있다면
[1,2,3] 4 [5,6] 7 [8,9]
[1,2,3] 이 배치될 수 있는 경우의 수 * [5,6] 이 배치 될 수 있는 경우의 수 * [8,9] 가 배치 될 수 있는 경우의 수 =
3*2*2 = 12이다
seat_count = 9
vip_seat_array = [4, 7]
number_of_cases_where_a_person_can_sit = {
1:1,
2:2,
}
def Fibo(n):
if n in number_of_cases_where_a_person_can_sit:
return number_of_cases_where_a_person_can_sit[n]
if len(list(filter(lambda k : k in number_of_cases_where_a_person_can_sit.keys(), [n - 1, n - 2]))) > 1:
number_of_cases_where_a_person_can_sit[n] = number_of_cases_where_a_person_can_sit[n - 1] + number_of_cases_where_a_person_can_sit[n - 2]
return Fibo(n - 1) + Fibo(n - 2)
def get_all_ways_of_theater_seat(total_count, fixed_seat_array):
array = []
result = 1
count = 0
for i in range (total_count):
array.append(i + 1)
while array:
if array.pop(0) in fixed_seat_array:
result *= Fibo(count)
count = 0
else :
count += 1
if count != 0:
result *= Fibo(count)
return result
# 12가 출력되어야 합니다!
print(get_all_ways_of_theater_seat(seat_count, vip_seat_array))
'GD프로젝트 > 개발일지' 카테고리의 다른 글
| 개발자 취업 필수 개념 1주차 개발일지(의미 있는 이름, 추상화, 예외, 리팩토링) (0) | 2021.08.19 |
|---|---|
| 알고보면 알기쉬운 알고리즘 - 5주차 개발일지(라인, 카카오, 삼성 코딩테스) (1) | 2021.08.16 |
| 알고보면 알기쉬운 알고리즘 - 3주차 개발일지(정렬, 스택, 큐, 해쉬) (0) | 2021.08.09 |
| 알고보면 알기쉬운 알고리즘 - 2주차 개발일지(Array, LinkedList, 이진 탐색, 재귀 함수) (0) | 2021.08.07 |
| 알고보면 알기쉬운 알고리즘 - 1주차 개발일지(시간복잡도, 공간복잡도, 점근 표기법) (0) | 2021.08.04 |




