책 읽다가 코딩하다 죽을래
알고보면 알기쉬운 알고리즘 - 2주차 개발일지(Array, LinkedList, 이진 탐색, 재귀 함수) 본문
GD프로젝트 알고리즘 수업 2주 차가 시작되었다.
그럼 2주 차에 배운 내용과 풀었던 알고리즘 문제에 대해 설명하겠다.
목차
1. 새롭게 배운 내용(Array, LinkedList, 이진 탐색, 재귀 함수)
2. 재귀 함수 문제
1. 새롭게 배운 내용
1. Array vs LinkedList
자료구조 중에서 자주 쓰이는 Array와 LInkedList를 서로 비교하겠다.
언어는 Python 기준으로 하겠다.
(선언할 때 배열 크기를 정해야 하는 c++, 자바의 정적 배열과는 달리 Python의 배열은 동적 배열이다.)
다음 간단한 배열의 예를 들어보자

배열은 index와 데이터로 이루어져있다.
index는 0으로부터 시작되며 데이터의 순서를 매기며
데이터는 int형부터 시작되어 그 어떤 데이터 타입도 들어갈 수 있다.
여기서 배열의 어떤 하나의 데이터에 접근하는데 걸리는 시간은 얼마나 소요될까?
정확히 말하자면 시간복잡도 O는 얼마일까?
답은 O(1)이다.
내가 접근하고 싶은 데이터가 배열의 맨 앞에 있는 뒤에 있든 중간에 있는
ary[0], ary[2], ary[4] 이런 식으로 단 한 번에 접근하기 때문이다.
배열 크기의 상관없이 배열 요소 접근 시간 복잡도는 O(1)이다.
그렇다면 삽입/삭제는 어떨까??
배열의 3번째 칸에 10이라는 데이터를 삽입한다고 가정해보자

3번째 칸에 10이라는 데이터를 추가하려면
이미 3번째 칸에 있는 3은 어떻게 해야 할까?
당연히 한 칸 뒤로 보내야 한다.
그렇다면 그 뒤에 있었던 데이터는 한 칸 더 뒤로 보내야 한다.

이런 식으로 말이다.
삭제의 경우는 어떨까?
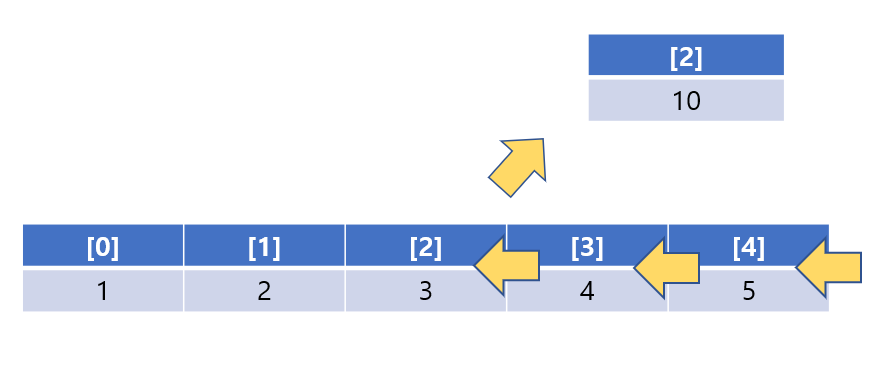
삭제의 경우도 마찬가지이다.
지워야 할 인덱스 뒤에 있는 데이터들은 한 칸씩 앞으로 당겨와야 한다.
그나마 배열의 맨 뒤에 요소를 추가하거나 삭제하는 것은 마지막 인덱스만 지우면 되니까 O(1)의 시간이 걸리지만
배열의 맨 앞에 요소를 추가하거나 삭제하는 것은 배열의 크기의 인덱스만큼을 앞으로 밀거나 당겨와야 하니
O(N)의 시간이 걸린다.
하지만 최악의 경우를 생각해야 하니 배열의 삽입/삭제의 시간복잡도는
O(N)이다
그다음은 LinkedList를 보겠다.

LinkedList는 다음과 같으며 코드는 이와 같다
class Node:
def __init__(self, data):
self.data = data
self.next = None
class LinkedList:
def __init__(self, value):
self.head = Node(value)
def append(self, value):
cur = self.head
while cur.next is not None:
cur = cur.next
cur.next = Node(value)
linked_list = LinkedList(1)
linked_list.append(2)
linked_list.append(3)
linked_list.append(4)
Linkedlist는 데이터와 노드로 이루어져 있다.
노드가 다음 번째 데이터를 가리키고 있어 인덱스와 똑같이
데이터의 순서가 있다.
하지만 차이점은 접근 방식에 있는데
Linkedlist의 요소 접근 시간복잡도는 O(N)이다.
그 이유는 기차를 생각하면 된다.
기차에 첫 번째 칸에서 마지막 칸으로 이동하는 방법은
첫 번째 칸에서 두 번째 칸으로 가고 그렇게 마지막 칸까지 가는 법이다.
배열처럼 데이터들의 위치가 인덱스로 정해져 있는 것이 아닌
데이터들이 노드로 이루어져 있기 때문에
맨 앞에 있는 데이터를 찾으려면 O(1)이 걸리지만
맨 뒤에 있는 데이터를 찾으려면 O(N)이 걸린다.
결과적으로 접근 시간복잡도는 O(N)이 걸린다.
삽입/삭제는 어떨까?

삽입/삭제는 해당 요소의 노드를 추가시켜 앞의 노드만 다르게 해 주면 된다.
즉 맨 앞에 추가하든 뒤에 추가하든 O(1)의 시간이 걸린다.
삭제 과정도 이와 유사하다.

삭제도 삭제할 요소 바로 앞의 노드만 고치면 된다.
LinkedList의 삽입/삭제의 시간복잡도는 O(1)이다.
이 둘의 자료구조를 정리하자면 다음과 같다.
| Array | LinkedList | |
| 특정 요소 접근 | O(1) | O(N) |
| 요소 삽입/삭제 | O(N) | O(1) |
| 데이터 추가 | 데이터 추가 시 모든 공간이 다 차버리면 새로운 메모리 공간을 할당받아야 한다 | 모든 공간이 다 찼어도 맨 뒤의 노드만 동적으로 추가하면 된다. |
| 요약 | 데이터에 접근하는 경우가 많다면 Array를 사용 | 삽입과 삭제가 빈번하다면 LinkedList를 사용 |
2. 이진 탐색

이런 배열이 있고 나는 'mango'라는 단어가 이 배열에 있는지 탐색한다고 가정하자
배열에 어느 특정 값을 찾으려면 당연히 처음부터 끝까지 하나씩 하나씩 찾아봐야 한다.
마치 배열 요소 닫힌 박스라고 생각하고 거기서 망고가 들어있는 박스를 찾으려면
하나하나씩 일일이 다 열어봐야 한다.
우린 이렇게 처음부터 순차적으로 데이터를 찾아보는 것을
순차 탐색이라 부른다.
여기서 운이 좋게도 한 번에 그 박스를 찾으면 행복하겠지만
맨 마지막에 그 박스를 찾으면 나는 운이 더럽게도 없다며 생각할 것이다.
여기서 순차 탐색의 시간복잡도를 알 수 있다.
찾고자 하는 데이터가 배열의 맨 앞에 있다면 시간 복잡도는 O(1)이지만
맨 뒤에 있었다면 시간복잡도는 O(N)이 걸릴 것이다.
즉 배열의 크기가 클수록 더 많은 시간이 걸린다.
여기서 시간복잡도가 O(logN) 이진 탐색을 설명하겠다.
이진 탐색은 오름차순으로 정렬된 배열에서 특정한 값의 위치를 찾는 알고리즘이다.

이진 탐색의 시작은 배열에서 가운데 인덱스에 접근하는 것이다.
그리고 그 인덱스에 값과 찾고자 하는 데이터의 크기 비교를 한다.
mango < melon
melon이 사전적으로 뒤에 위치하므로
내가 찾고자 하는 데이터보다 크다.
그럼 melon보다 뒤에 있는 데이터들은
찾아보지 않아도 mango보다 크다는 것을 아니까
굳이 탐색할 필요가 없다.
(왜냐하면 배열은 지금 오름차순으로 정렬되어 있기 때문이다.)
그러면 melon과 함께 그 뒤에 있는 데이터들은 용의 선상에서 제외하면 된다.

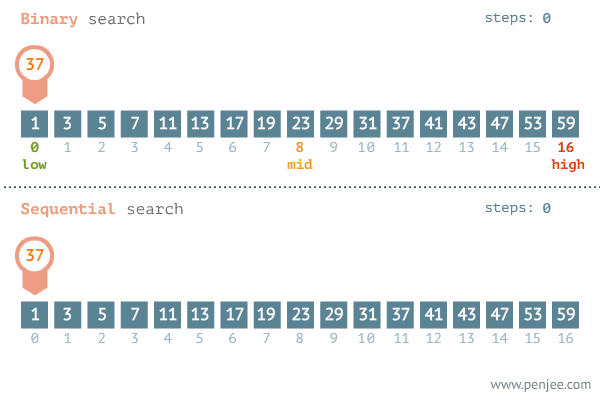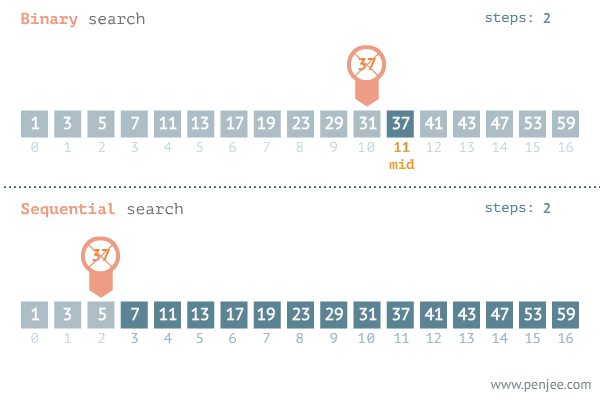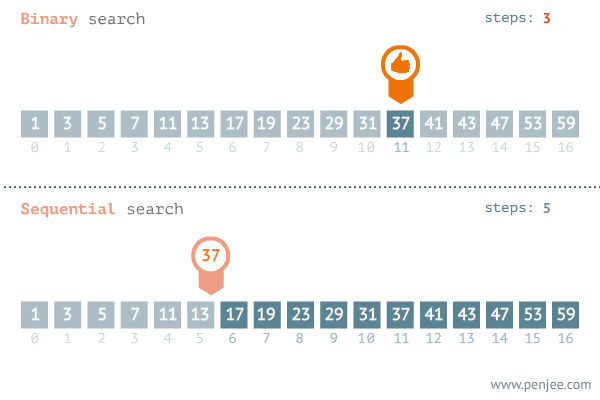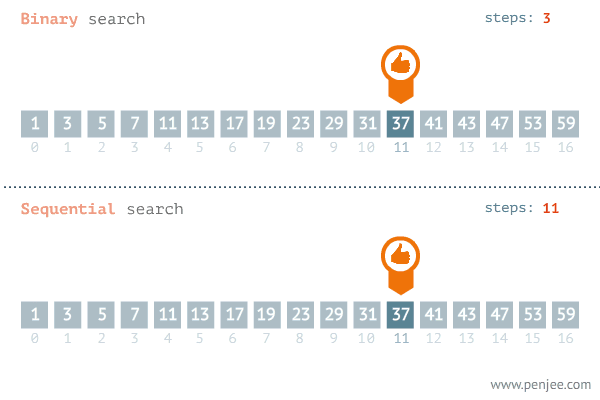
그다음 남아있는 배열의 요소에서 가운데 인덱스에 접근한다.
아까처럼 가운데 인덱스의 값과 찾고자 하는 값을 비교하여
가운데 인덱스가 더 크면 왼쪽의 요소들만
더 작으면 오른쪽의 요소들만 찾으면 되는 것이다.
mango는 grape보다 더 작으므로
왼쪽의 요소들은 용의 선상에서 제외하면 된다.

우리는 이렇게 단 3번 만의 데이터를 찾았다.
이진 탐색의 방법을 이해했다면 이제 시간복잡도를 구해보자
우리가 찾고 싶은 배열의 크기가 N이라고 한다면
이진 탐색으로 1번 탐색하면 반절이 줄어드니 N/2 개가 남는다.
2번 탐색하면 반절이 줄어드니 N/4 = N/2² 개가 남는다.
3번 탐색하면 반절이 줄어드니 N/8 = N/2³ 개가 남는다.
...
k번 탐색하면 반절이 줄어드니 N/2^k 개가 남는다
이때 이진 탐색을 열심히 시도해서 딱 1개만 남았다고 가정하면
N/2^k = 1 가 된다.
즉 k = log₂N 횟수를 시도하면 되는 것이다.
이진 탐색은 시간 복잡도가 O(logN) 만큼 걸린다.
왜 O(log₂N)이 아닌 이유는 시간복잡도 특성상 상수는 무시하기 때문입니다.
그러면 이진 탐색은 순차 탐색보다 무조건 빠르니 적극적으로 이용해야겠군요??
그건 아니다. 앞에서 보시다시피 이진 탐색을 하려면 배열이 오름차순이든 내림차순이든 정렬이 되어있어야 한다. 순차 탐색은 이러한 과정 없이 O(N)이 걸리는데 이진 탐색은 배열이 정렬이 되어있다는 전제하에 O(logN)이라는 것이다.
상황에 맞게 적절히 고르면 될 것이다.
3. 재귀 함수
재귀 함수는 함수 안에 자기를 다시 호출하는 함수이다.
알고리즘 문제 중 어떤 패턴이 반복적으로 나오거나, 같은 문제를 여러 번 풀어야 하는 상황이 생길 때
쓰이는 방법이다.
재귀 함수를 만드는 방법은 간단하다.
def infinity:
print("재귀함수가 뭐냐면은...")
infinity()
함수 안에 다시 자신의 함수를 호출하면 된다.
근데 위의 예시는 계속 자신의 함수를 무한정 호출하게 되므로
스택오버플로우 오류가 일어난다.
def function(k):
if k <= 0 : return # Base case : 적어도 하나의 recursion에 빠지지 않는 경우가 존재해야 한다
else : # Recursive case : recursion을 반복하다보면 결국 Base case로 수렴해야 한다.
print("재귀함수가 뭐냐면은...")
function(k - 1)
function(10)
스택오버플로우가 일어나지 않게 하려면
재귀 함수 내에 재귀 함수를 벗어나는 Base case라는 조건문이 있어야 한다.
마치 무한 반복문을 피하기 위해 조건문을 적는 것과 똑같다.
그러면 재귀 함수의 대표적인 사용 사례인 팩토리얼 알고리즘을 보자
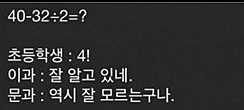
팩토리얼은 1부터 어떤 양의 정수 N까지의 정수를 모두 곱한 것을 의미한다.
예로 들면
3! 은 3 * 2 * 1 = 6
4! 은 4 * 3 * 2 * 1 = 24
그래서 40-32/2 = 24 = 4! 이므로 4!라고 대답한 초등학생의 답도 맞는다는 것이다.
여기서
3! 은 3 * 2 * 1 = 6
4! 은 4 * 3 * 2 * 1 = 24
팩토리얼을 구하는 과정을 보면
Factorial(n) = n * Factorial(n - 1)
Factorial(n - 1) = (n - 1) * Factorial(n - 2)
...
Factorial(1) = 1
라는 구조가 보일 것이다.
4! 를 예로 들면
Factorial(4) = 4 * Factorial(3)
Factorial(3) = 3 * Factorial(2)
Factorial(2) = 2 * Factorial(1)
Factorial(1) = 1
이래도 잘 이해가 안 가시면
하나씩 풀어보면 된다.
Factorial(4) = 4 * Factorial(3)
Factorial(4) = 4 * 3 * Factorial(2)
Factorial(4) = 4 * 3 * 2 * Factorial(1)
Factorial(4) = 4 * 3 * 2 * 1
이것을 재귀 함수 코드로 나타내면 다음과 같다
def factorial(n):
if n == 1:
return 1
return n * factorial(n - 1)
print(factorial(4)) # 24 출력
코드가 어떻게 동작하는지 어렵다면 디버깅을 꼭 해보길 바란다.
2. 재귀 함수 문제

numbers = [1, 1, 1, 1, 1]
target_number = 3
def get_count_of_ways_to_target_by_doing_plus_or_minus(array, target):
# 구현해보자
return
print(get_count_of_ways_to_target_by_doing_plus_or_minus(numbers, target_number)) # 5가 나와야한다
이번 주차에 3문제를 풀었는데
유일하게 못 풀었던 문제이다.
예시가 number는 [1,1,1,1,1], target_number는 3으로 헷갈릴 수가 있어
number = [2,3,1], target_number = 0으로 생각해보고 다시 풀어보자
일단 2,3,1을 연산해서 나올 수 있는 모든 경우의 수를 생각해보자
1. +2 +3 +1 = 6
2. +2 +3 -1 = 4
3. +2 -3 +1 = 0 # 타겟!
4. +2 -3 -1 = -2
5. -2 +3 +1 = 2
6. -2 +3 -1 = 0 # 타겟!
7. -2 -3 +1 = -4
8. -2 -3 -1 = -7
이 경우의 수에서 반복되는 패턴을 찾아야 한다.
여기서 각 경우의 수에 +-연산자만 확인하자
1. +++
2. ++-
3. +-+
4. +--
5. -++
6. -+-
7. --+
8. ---
패턴이 보이나요?
정확히 말하자면
N의 길이의 배열에서 더하거나 뺀 모든 경우의 수는
N - 1의 길이의 배열에서 마지막 원소를 더하거나 뺀 경우의 수를
추가하시면 된다.
이게 무슨 말이냐면
[2,3]을 배치하는 모든 경우의 수는
맨 마지막 원소인 1을 더하나 빼냐에 따라서 [2,3,1]의 경우의 수를 구할 수 있다는 것이다.
즉 계속 문제를 잘게 쪼개는 것이다.
더 이상 쪼개지지 못하는 크기로 잘게 쪼개 놓은 다음
그 문제들을 하나씩 풀어서 붙이는 것이다.
다시 [2, 3] 을 배치하는 모든 경우의 수는 다음과 같다.
1. +2 +3
2. +2 -3
3. -2 +3
4. -2 -3
여기서 1을 더하느냐 빼냐에 따라 경우의 수가 다음과 같이 생긴다.
1. +2 +3 → +1 = +2 +3 +1
→ -1 = +2 +3 -1
2. +2 -3 → +1 = +2 -3 +1
→ -1 = +2 +3 -1
3. -2 +3 → +1 = -2 +3 +1
→ -1 = -2 +3 -1
4. -2 -3 → +1 = -2 -3 +1
→ -1 = -2 -3 -1
하나씩 원소를 추가할 때마다
새로 추가된 원소를 더하고 빼는 경우의 수를 추가하면 된다.
numbers = [1, 1, 1, 1, 1]
target_number = 3
result_count = 0
# N의 길이의 배열에서 더하거나 뺀 모든 경우의 수는
# N - 1의 길이의 배열에서 마지막 원소를 더하거나 뺀 경우의 수를
# 추가하시면 됩니다.
def get_count_of_ways_to_target_by_doing_plus_or_minus(array, target, current_index, current_sum):
if current_index == len(array):
if current_sum == target:
global result_count
result_count += 1
return
get_count_of_ways_to_target_by_doing_plus_or_minus(array, target, current_index + 1, current_sum + array[current_index])
get_count_of_ways_to_target_by_doing_plus_or_minus(array, target, current_index + 1, current_sum - array[current_index])
get_count_of_ways_to_target_by_doing_plus_or_minus(numbers, target_number, 0, 0)
print(result_count)
정답 코드는 다음과 같다.
위의 코드는 get_count_of_ways_to_target_by_doing_plus_or_minus 함수 안에 (이하 get_count로 명명)
get_count를 다음 요소와 + 한 상태와 -1 한 상태로 다시 불러오는 것이다.
current_index가 배열의 길이와 똑같다면 끝까지 더하고 뺀 것이니
그때 나온 current_sum이 target가 똑같다면 count를 세주는 코드이다.
나는 계속 recursive case에 자기 함수를 한 번밖에 호출 못한다는 생각 때문에 못 풀었던 것 같았다.
재귀 함수는 자신의 함수 안에 여러 번 호출할 수 있다는 것도 중요한 것 같다.
'GD프로젝트 > 개발일지' 카테고리의 다른 글
| 알고보면 알기쉬운 알고리즘 - 4주차 개발일지(트리, 힙, 그래프, DFS&BFS, DP) (0) | 2021.08.11 |
|---|---|
| 알고보면 알기쉬운 알고리즘 - 3주차 개발일지(정렬, 스택, 큐, 해쉬) (0) | 2021.08.09 |
| 알고보면 알기쉬운 알고리즘 - 1주차 개발일지(시간복잡도, 공간복잡도, 점근 표기법) (0) | 2021.08.04 |
| 리액트 심화반 - 5주차 개발일지(SEO, 웹 성능 지표) (0) | 2021.08.02 |
| 리액트 심화반 - 4주차 개발일지(Badge, RealTimeBase) (0) | 2021.08.01 |




